Podrobne sú uvažované príklady riešenia integrálov po častiach, ktorých integrand je súčinom polynómu exponentom (e k mocnine x) alebo sínusom (sin x) alebo kosínusom (cos x).

Obsah

Pozri tiež: Integrácia po častiach
Neurčitá integrálna tabuľka
Metódy výpočtu neurčitých integrálov
Základné elementárne funkcie a ich vlastnosti

Vzorec integrácie podľa častí

Pri riešení príkladov v tejto časti sa používa vzorec integrácie podľa častí:
;
.

Príklady integrálov obsahujúcich súčin polynómu a sin x, cos x alebo e x

Tu sú príklady takýchto integrálov:
, , .

Na integráciu takýchto integrálov je polynóm označený u a zvyšok - v dx. Ďalej sa použije vzorec pre integráciu po častiach.

Nižšie je uvedené podrobné riešenie týchto príkladov.

Príklady integrálnych riešení

Príklad s exponentom, e na x mocnine

Určte integrál:
.

Zaveďme exponent pod diferenciálne znamienko:
e - x dx = - e - x d (-x) = - d (e - x).

Integrujeme po častiach.

tu
.
Zostávajúci integrál je tiež integrovateľný po častiach.
.
.
.
Nakoniec tu máme:
.

Príklad definovania integrálu so sínusom

Vypočítajte integrál:
.

Zavedme sínus pod znamienkom diferenciálu:

Integrujeme po častiach.

tu u = x 2, v = cos (2 x + 3), du = ( x 2 )′ dx

Zostávajúci integrál je tiež integrovateľný po častiach. Aby sme to dosiahli, zavedieme kosínus pod znamienko diferenciálu.

tu u = x, v = hriech (2 x + 3), du = dx

Nakoniec tu máme:

Príklad súčinu polynómu a kosínusu

Vypočítajte integrál:
.

Predstavme si kosínus pod znamienkom diferenciálu:

Integrujeme po častiach.

tu u = x 2 + 3 x + 5, v = hriech 2x, du = ( x 2 + 3 x + 5 )′ dx

Chýbať nebudú ani úlohy na samostatné riešenie, na ktoré si môžete pozrieť odpovede.

Integrand možno previesť zo súčinu goniometrických funkcií na súčet

Uvažujme integrály, v ktorých je integrand súčinom sínusov a kosínusov prvého stupňa x, vynásobených rôznymi faktormi, teda integrálmi tvaru

Pomocou známych trigonometrických vzorcov

(2)
(3)
(4)
každý zo súčinov integrálu tvaru (31) možno previesť na algebraický súčet a integrovať pomocou vzorcov

(5)

(6)

Príklad 1 Nájsť

Riešenie. Podľa vzorca (2) at

Príklad 2 Nájsť integrál goniometrickej funkcie

Riešenie. Podľa vzorca (3) at

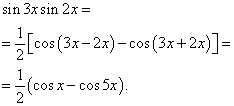
Príklad 3 Nájsť integrál goniometrickej funkcie

Riešenie. Podľa vzorca (4) at získame nasledujúcu transformáciu integrandu:

Aplikovaním vzorca (6) dostaneme

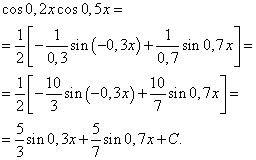
Integrál súčinu mocnín sínusu a kosínusu toho istého argumentu

Uvažujme teraz integrály funkcií, ktoré sú súčinom mocnín sínusu a kosínusu toho istého argumentu, t.j.

(7)

V konkrétnych prípadoch jeden z ukazovateľov ( m alebo n) môže byť nula.

Pri integrácii takýchto funkcií sa používa, že párny stupeň kosínusu možno vyjadriť ako sínus a sínusový diferenciál sa rovná cos. x dx(alebo párny stupeň sínusu možno vyjadriť pomocou kosínusu a diferenciál kosínusu je - sin x dx ) .

Treba rozlišovať dva prípady: 1) aspoň jeden z ukazovateľov m a n zvláštny; 2) oba ukazovatele sú párne.

Nech sa uskutoční prvý prípad, a to exponent n = 2k+ 1 je nepárne. Potom, vzhľadom na to

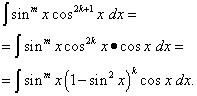
Integrand je prezentovaný tak, že jedna jeho časť je funkciou iba sínusu a druhá je diferenciálom sínusu. Teraz s variabilnou substitúciou t= hriech X riešenie sa redukuje na integráciu polynómu vzhľadom na t... Keby len stupeň m je nepárne, potom postupujte rovnakým spôsobom, oddeľte faktor sin X, vyjadrujúci zvyšok integrandu v termínoch cos X a za predpokladu t= čos X... Túto techniku je možné použiť na integrácia kvocientových mocnín sínusu a kosínusu , kedy aspoň jeden z ukazovateľov je nepárny ... Ide o to, že kvocient stupňov sínusu a kosínusu je špeciálnym prípadom ich súčinu : keď je goniometrická funkcia v menovateli integrandu, jej stupeň je záporný. Existujú však aj prípady konkrétnych goniometrických funkcií, ktorých stupne sú len párne. O nich - nasledujúci odsek.

Ak oba ukazovatele m a n- párne, potom pomocou goniometrických vzorcov

znížiť exponenty sínusu a kosínusu, po čom sa získa integrál rovnakého typu ako vyššie. Preto by integrácia mala pokračovať rovnakým spôsobom. Ak je jeden z párnych indikátorov negatívny, to znamená, že sa berie do úvahy kvocient párnych stupňov sínusu a kosínusu, potom táto schéma nie je vhodná. ... Potom sa použije variabilná substitúcia v závislosti od toho, ako sa dá integrand transformovať. Takýmto prípadom sa budeme zaoberať v ďalšej časti.

Príklad 4 Nájsť integrál goniometrickej funkcie

Riešenie. Exponent kosínusu je nepárny. Preto zastupujeme

t= hriech X(potom dt= čos X dx ). Potom dostaneme

Keď sa vrátime k starej premennej, konečne nájdeme

Príklad 5. Nájsť integrál goniometrickej funkcie

Riešenie. Exponent kosínusu, ako v predchádzajúcom príklade, je nepárny, ale viac. Predstavte si

a zmeniť premennú t= hriech X(potom dt= čos X dx ). Potom dostaneme

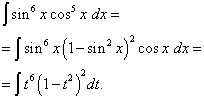
Rozšírime zátvorky

a získať

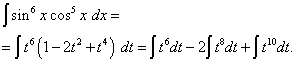
Keď sa vrátime k starej premennej, dostaneme riešenie

Príklad 6. Nájsť integrál goniometrickej funkcie

Riešenie. Sínusové a kosínusové exponenty sú párne. Preto transformujeme integrand takto:

Potom dostaneme

V druhom integráli meníme premennú nastavením t= hriech2 X... Potom (1/2)dt= cos2 X dx ... teda

Konečne sa dostávame

Použitie metódy variabilnej náhrady

Variabilná metóda výmeny pri integrácii goniometrických funkcií sa dá použiť v prípadoch, keď je v integrande prítomný iba sínus alebo iba kosínus, súčin sínusu a kosínusu, v ktorom je buď sínus alebo kosínus v prvej mocnine, dotyčnici alebo kotangens, ako aj podiel párnych mocnín sínusu a kosínusu jedného a toho istého argumentu. V tomto prípade je možné vykonávať permutácie nielen hriechu X = t a hriech X = t ale aj tg X = t a ctg X = t .

Príklad 8. Nájsť integrál goniometrickej funkcie

Riešenie. Zmeňme teda premennú:. Výsledný integrand sa ľahko integruje cez tabuľku integrálov:

Príklad 9. Nájsť integrál goniometrickej funkcie

Riešenie. Transformujeme dotyčnicu na pomer sínusu a kosínusu:

Zmeňme teda premennú:. Výsledný integrand je tabuľkový integrál so znamienkom mínus:

Keď sa vrátime k pôvodnej premennej, nakoniec dostaneme:

Príklad 10. Nájsť integrál goniometrickej funkcie

Riešenie. Zmeňme teda premennú:.

Transformujeme integrand na uplatnenie trigonometrickej identity :

Zmeníme premennú, pričom nezabudneme dať pred integrál znamienko mínus (pozri vyššie, čo sa rovná dt). Ďalej rozšírime integrand na faktory a integrujeme cez tabuľku:

Keď sa vrátime k pôvodnej premennej, nakoniec dostaneme:

Nájdite integrál goniometrickej funkcie sami a potom uvidíte riešenie

Generická trigonometrická substitúcia

Univerzálna trigonometrická substitúcia možno použiť v prípadoch, keď integrand nezodpovedá prípadom uvedeným v predchádzajúcich odsekoch. V zásade vtedy, keď sú sínus alebo kosínus (alebo oboje) v menovateli zlomku. Je dokázané, že sínus a kosínus možno nahradiť iným výrazom obsahujúcim tangens polovice pôvodného uhla takto:

Všimnite si však, že univerzálna trigonometrická substitúcia často zahŕňa pomerne zložité algebraické transformácie, takže je lepšie ju použiť, keď žiadna iná metóda nefunguje. Pozrime sa na príklady, keď sa spolu s univerzálnou goniometrickou substitúciou použije súčet pod diferenciálnym znamienkom a metóda nedefinovaných koeficientov.

Príklad 12. Nájsť integrál goniometrickej funkcie

Riešenie. Riešenie. Budeme používať univerzálna trigonometrická substitúcia... Potom
.

Zlomky v čitateli a menovateli vynásobíme a dva odsunieme a dáme pred znamienko integrálu. Potom

Na integráciu racionálnych funkcií tvaru R (sin x, cos x) sa používa substitúcia, ktorá sa nazýva univerzálna trigonometrická substitúcia. Potom . Generická trigonometrická substitúcia je často výpočtovo náročná. Preto vždy, keď je to možné, používajte nasledujúce náhrady.

Integrácia funkcií racionálne v závislosti od goniometrických funkcií

1. Integrály tvaru ∫ sin n xdx, ∫ cos n xdx, n > 0
a) Ak je n nepárne, potom jeden stupeň sinx (alebo cosx) by sa mal zadať pod znamienkom diferenciálu a od zvyšného párneho stupňa by sa malo prejsť na opačnú funkciu.
b) Ak je n párne, potom použijeme vzorce na zníženie stupňa
2. Integrály tvaru ∫ tg n xdx, ∫ ctg n xdx, kde n je celé číslo.
Musíte použiť vzorce

3. Integrály tvaru ∫ sin n x · cos m x dx
a) Nech m a n majú rôznu paritu. Aplikujeme substitúciu t = sin x, ak je n nepárne, alebo t = cos x, ak je m nepárne.
b) Ak sú m a n párne, potom použijeme vzorce na zníženie stupňa
2sin 2 x = 1-cos2x, 2cos 2 x = 1 + cos2x.
4. Integrály formulára

Ak čísla m a n majú rovnakú paritu, potom použijeme substitúciu t = tg x. Často je vhodné použiť techniku trigonometrických jednotiek.
5.∫ sin (nx) cos (mx) dx, ∫ cos (mx) cos (nx) dx, ∫ sin (mx) sin (nx) dx

Na prevod súčinu goniometrických funkcií na ich súčet použijeme vzorce:

sin α cos β = ½ (sin (α + β) + sin (α-β))
cos α cos β = ½ (cos (α + β) + cos (α-β))
sin α sin β = ½ (cos (α-β) -cos (α + β))

Príklady
1. Vyhodnoťte integrál ∫ cos 4 x · sin 3 xdx.
Urobíme substitúciu cos (x) = t. Potom ∫ cos 4 x sin 3 xdx =
2. Vypočítajte integrál.
Ak urobíme zmenu sin x = t, dostaneme

3. Nájdite integrál.
Urobíme zmenu tg (x) = t. Nahradením dostaneme

Integrácia výrazov ako R (sinx, cosx)

Príklad #1. Vypočítajte integrály:

Riešenie.
a) Integrácia výrazov tvaru R (sinx, cosx), kde R je racionálna funkcia sin x a cos x, sa transformujú na integrály racionálnych funkcií pomocou univerzálnej goniometrickej substitúcie tg (x / 2) = t.
Potom máme

Univerzálna goniometrická substitúcia umožňuje prejsť od integrálu v tvare ∫ R (sinx, cosx) dx k integrálu zlomkovej racionálnej funkcie, často však takáto substitúcia vedie k ťažkopádnym výrazom. Za určitých podmienok sú jednoduchšie náhrady účinné:

Ak platí rovnosť R (-sin x, cos x) = -R (sin x, cos x) dx, použije sa substitúcia cos x = t.
Ak platí rovnosť R (sin x, -cos x) = -R (sin x, cos x) dx, potom substitúcia sin x = t.
Ak platí rovnosť R (-sin x, -cos x) = R (sin x, cos x) dx, potom substitúcia tgx = t alebo ctg x = t.

V tomto prípade nájsť integrál

použiť univerzálnu goniometrickú substitúciu tg (x / 2) = t.
Potom je odpoveď:

Integrály goniometrických funkcií.
Príklady riešení

V tejto lekcii sa budeme zaoberať integrálmi goniometrických funkcií, to znamená, že výplňou integrálov budú sínusy, kosínusy, tangens a kotangens v rôznych kombináciách. Všetky príklady budú podrobne rozobraté, dostupné a zrozumiteľné aj pre čajník.

Ak chcete úspešne študovať integrály goniometrických funkcií, musíte poznať najjednoduchšie integrály a ovládať niektoré integračné techniky. S týmito materiálmi sa môžete zoznámiť na prednáškach Neurčitý integrál. Príklady riešení a .

A teraz potrebujeme: Integrálny stôl, Tabuľka derivátov a Odkaz na trigonometrický vzorec... Všetky učebné pomôcky nájdete na stránke Matematické vzorce a tabuľky... Odporúčam všetko vytlačiť. Zameriavam sa najmä na trigonometrické vzorce, mali by byť pred vašimi očami- bez toho sa efektivita práce výrazne zníži.

Najprv však o tom, ktoré integrály v tomto článku nie... Neexistujú žiadne integrály formulára - kosínus, sínus, násobený nejakým polynómom (menej často niečo s tangensom alebo kotangensom). Takéto integrály sú integrované po častiach a ak sa chcete naučiť metódu, navštívte lekciu Integrácia po častiach. Príklady riešení.Neexistujú ani integrály s "oblúkmi" - arktangens, arcsínus atď., tie sú tiež najčastejšie integrované po častiach.

Pri hľadaní integrálov goniometrických funkcií sa používa niekoľko metód:

(4) Používame tabuľkový vzorec , rozdiel je len v tom, že namiesto "x" máme zložitý výraz.

Príklad 2

Príklad 3

Nájdite neurčitý integrál.

Klasika žánru pre tých, ktorí sa topia v teste. Ako ste si pravdepodobne všimli, v tabuľke integrálov nie je integrál tangens a kotangens, ale napriek tomu takéto integrály možno nájsť.

(1) Používame trigonometrický vzorec

(2) Funkciu privedieme pod znamienko diferenciálu.

(3) Používame tabuľkový integrál .

Príklad 4

Nájdite neurčitý integrál.

Toto je príklad samostatného riešenia, úplného riešenia a odpovede - na konci lekcie.

Príklad 5

Nájdite neurčitý integrál.

Naše stupne budú postupne pribúdať =).
Najprv riešenie:

(1) Používame vzorec

(2) Používame základnú goniometrickú identitu , z čoho vyplýva, že .

(3) Člen čitateľa vydeľte menovateľom.

(4) Používame vlastnosť linearity neurčitého integrálu.

(5) Integrujeme pomocou tabuľky.

Príklad 6

Nájdite neurčitý integrál.

Toto je príklad samostatného riešenia, úplného riešenia a odpovede - na konci lekcie.

Existujú aj integrály dotyčníc a kotangens, ktoré sú vo vyšších stupňoch. V lekcii sa uvažuje s integrálom dotyčnice v kocke Ako vypočítam plochu plochej postavy? Integrály dotyčnice (kotangens) v štvrtom a piatom stupni nájdete na stránke Komplexné integrály.

Zníženie stupňa integrandu

Táto technika funguje, keď sú integrandy naplnené sínusmi a kosínusmi dokonca stupňa. Na zníženie stupňa sa používajú trigonometrické vzorce , a navyše posledný vzorec sa častejšie používa v opačnom smere: .

Príklad 7

Nájdite neurčitý integrál.

Riešenie:

V podstate tu nie je nič nové, okrem toho, že sme použili vzorec (znížením stupňa integrandu). Upozorňujeme, že riešenie som skrátil. S nahromadením skúseností možno integrál nájsť ústne, čo šetrí čas a je celkom prijateľné pri dokončovaní úloh. V tomto prípade je vhodné pravidlo nepopisovať , najprv ústne berieme integrál 1, potom - of.

Príklad 8

Nájdite neurčitý integrál.

Toto je príklad samostatného riešenia, úplného riešenia a odpovede - na konci lekcie.

Toto sú sľúbené zvýšenie stupňa:

Príklad 9

Nájdite neurčitý integrál.

Najprv riešenie, potom komentáre:

(1) Pripravte integrand na použitie vzorca .

(2) V skutočnosti použijeme vzorec.

(3) Odmocníme menovateľa a posunieme konštantu mimo znamienka integrálu. Dalo by sa konať trochu inak, ale podľa mňa je to takto pohodlnejšie.

(4) Používame vzorec

(5) V treťom termíne opäť znížime stupeň, ale tentoraz pomocou vzorca .

(6) Uvádzame podobné výrazy (tu delím podľa výrazov a urobil sčítanie).

(7) V skutočnosti berieme integrál, pravidlo linearity a spôsob uvedenia funkcie pod diferenciálne znamienko sa vykonáva ústne.

(8) Skombinujte odpoveď.

! V neurčitom integráli môže byť odpoveď často napísaná niekoľkými spôsobmi

V práve uvažovanom príklade by mohla byť konečná odpoveď napísaná inak - rozšíriť zátvorky a dokonca to urobiť ešte pred integráciou výrazu, to znamená, že nasledujúci koniec príkladu je celkom prijateľný:

Je dosť možné, že táto možnosť je ešte výhodnejšia, len som to vysvetlil tak, ako som bol zvyknutý riešiť). Tu je ďalší typický príklad riešenia „urob si sám“:

Príklad 10

Nájdite neurčitý integrál.

Tento príklad sa dá vyriešiť dvoma spôsobmi a možno aj dostanete dve úplne odlišné odpovede(presnejšie budú vyzerať úplne inak a z matematického hľadiska budú rovnocenné). S najväčšou pravdepodobnosťou neuvidíte najracionálnejší spôsob a budete trpieť otváraním zátvoriek pomocou iných trigonometrických vzorcov. Najúčinnejšie riešenie je uvedené na konci lekcie.

Zhrnutím odseku dospejeme k záveru: akýkoľvek integrál formy , kde a - dokoncačíslo, sa rieši metódou znižovania stupňa integrandu.
V praxi som sa stretol s integrálmi s 8 a 10 stupňami a ich strašné hemoroidy som musel riešiť niekoľkonásobným znížením stupňa, čo malo za následok dlhé dlhé odpovede.

Variabilná metóda výmeny

Ako je spomenuté v článku Metóda zmeny premennej v neurčitom integráli, hlavným predpokladom použitia náhradnej metódy je skutočnosť, že v integrande je nejaká funkcia a jej derivácia:
(funkcie, ktoré nie sú nevyhnutne súčasťou produktu)

Príklad 11

Nájdite neurčitý integrál.

Pozeráme sa na tabuľku derivátov a všimneme si vzorce, , teda v našom integrande je funkcia a jej derivácia. Vidíme však, že pri diferenciácii sa kosínus a sínus vzájomne premieňajú na seba a vzniká otázka: ako zmeniť premennú a čo označiť - sínus alebo kosínus?! Otázku možno vyriešiť vedeckým šťouchnutím: ak výmenu vykonáme nesprávne, nepríde z toho nič dobré.

Všeobecný pokyn: v podobných prípadoch je potrebné určiť funkciu, ktorá je v menovateli.

Prerušíme riešenie a vymeníme

V menovateli je u nás všetko v poriadku, všetko závisí len od toho, teraz zostáva zistiť, na čo sa to zmení.
Aby sme to dosiahli, nájdeme diferenciál:

Alebo v skratke:
Zo získanej rovnosti podľa pravidla proporcie vyjadríme výraz, ktorý potrebujeme:

Takže:

Teraz celý integrand závisí len od a riešenie môže pokračovať

Pripravený. Dovoľte mi pripomenúť, že účelom výmeny je zjednodušenie integrandu, v tomto prípade sa to všetko zvrhlo na integráciu funkcie napájania cez stôl.

Nie je náhoda, že som tento príklad namaľoval tak podrobne, bolo to urobené s cieľom zopakovať a upevniť učebné materiály. Metóda zmeny premennej v neurčitom integráli.

A teraz dva príklady pre nezávislé riešenie:

Príklad 12

Nájdite neurčitý integrál.

Príklad 13

Nájdite neurčitý integrál.

Vyplňte riešenia a odpovede na konci hodiny.

Príklad 14

Nájdite neurčitý integrál.

Aj tu je v integrande sínus s kosínusom (funkcia s deriváciou), ale už v súčine a vzniká dilema - čo označiť, sínus alebo kosínus?

Môžete sa pokúsiť vykonať výmenu vedeckou metódou poke, a ak nič nefunguje, označte ju pre inú funkciu, ale existuje:

Všeobecný pokyn: pretože je potrebné označiť funkciu, ktorá je, obrazne povedané, v „nepohodlnej polohe“.

Vidíme, že v tomto príklade študentský kosínus "trpí" na stupeň a sínus sedí voľne sám o sebe.

Preto nahradíme:

Ak má niekto stále problémy s algoritmom nahrádzania premenných a hľadaním diferenciálu, mali by ste sa vrátiť k lekcii Metóda zmeny premennej v neurčitom integráli.

Príklad 15

Nájdite neurčitý integrál.

Analyzujeme integrand, čo by malo byť označené?
Pripomíname si naše orientačné body:
1) Funkcia je s najväčšou pravdepodobnosťou v menovateli;
2) Funkcia je v „nevhodnej polohe“.

Mimochodom, tieto pokyny platia nielen pre goniometrické funkcie.

Sínus vyhovuje obom kritériám (najmä druhému), preto sa navrhuje výmena. V zásade môže byť výmena už vykonaná, ale najprv by bolo pekné na to prísť, ale čo s tým robiť? Najprv „odtrhneme“ jeden kosínus:

Vyhradzujeme si pre náš "budúci" diferenciál

A vyjadrujeme cez sínus pomocou základnej goniometrickej identity:

Teraz je tu náhrada:

Všeobecné pravidlo: Ak je v integrande jedna z goniometrických funkcií (sínus alebo kosínus) v zvláštny stupňa, potom je potrebné "odhryznúť" jednu funkciu z nepárneho stupňa a určiť inú funkciu. Hovoríme len o integráloch, kde sú kosínusy a sínusy.

V uvažovanom príklade sme mali kosínus v nepárnom stupni, takže sme oddelili jeden kosínus od stupňa a označili sme sínus za.

Príklad 16

Nájdite neurčitý integrál.

Stupne uberajú =).
Toto je príklad riešenia „urob si sám“. Kompletné riešenie a odpoveď na konci tutoriálu.

Generická trigonometrická substitúcia

Všeobecná trigonometrická substitúcia je bežným prípadom variabilnej substitúcie. Môžete to skúsiť použiť, keď „neviete, čo máte robiť“. V skutočnosti však existujú určité pokyny na jeho aplikáciu. Typické integrály, kde musíte použiť univerzálnu goniometrickú substitúciu, sú tieto integrály: , , , atď.

Príklad 17

Nájdite neurčitý integrál.

V tomto prípade sa univerzálna trigonometrická substitúcia realizuje nasledujúcim spôsobom. Nahradíme:. Nepoužívam písmeno, ale písmeno, to nie je nejaké pravidlo, len som si zase zvykol riešiť.

Je pohodlnejšie nájsť diferenciál tu, preto z rovnosti vyjadrujem:
K obom častiam pripájam arkustangens:

Arkustangens a tangens sa navzájom rušia: