در این درس یاد خواهیم گرفت که تداوم یک تابع را ایجاد کنیم. ما این کار را با استفاده از محدودیت ها ، و یک طرفه - راست و چپ انجام خواهیم داد ، که علی رغم این که مثل و مثل نوشته شده اند ، اصلاً ترسناک نیستند.
اما تداوم یک تابع به طور کلی چیست؟ تا زمانی که به یک تعریف دقیق نرسیم ، ساده ترین تصور یک خط است که می تواند بدون برداشتن مداد از روی کاغذ ترسیم شود. اگر چنین خطی کشیده شود ، آنگاه پیوسته است. این خط نمودار یک تابع پیوسته است.
از نظر گرافیکی ، یک تابع در یک نقطه پیوسته است ، اگر نمودار آن در آن نقطه "شکسته نشود". نمودار چنین تابع مداوم - 
در شکل زیر نشان داده شده است.
تعیین تداوم یک تابع از طریق حد. در صورت تحقق سه شرط ، یک نقطه مداوم است:
1. تابع در یک نقطه تعریف می شود.
اگر حداقل یکی از شرایط ذکر شده برآورده نشود ، عملکرد در نقطه مداوم نیست. در این حالت ، آنها می گویند که تابع دچار شکست می شود و نقاط موجود در نمودار که نمودار در آن قطع شده است ، نقاط شکست تابع نامیده می شوند. نمودار چنین تابعی که در نقطه x \u003d 2 ناپیوسته باشد ، در شکل زیر نشان داده شده است.
مثال 1تابع f(ایکس) به شرح زیر تعریف می شود:
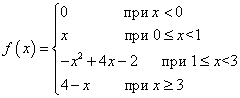
آیا این تابع در هر یک از نقاط مرزی شاخه های خود ، یعنی در نقاط ، پیوسته خواهد بود ایکس = 0 , ایکس = 1 , ایکس = 3 ?
تصمیم گیری ما هر سه شرط را برای تداوم عملکرد در هر نقطه مرزی بررسی می کنیم. شرط اول وجود دارد ، از آنجا که این واقعیت است که تابع تعریف شده است در هر یک از نقاط مرزی از تعریف تابع پیروی می شود. برای بررسی دو شرط دیگر باقی مانده است.
نقطه ایکس \u003d 0 حد دست چپ را در این مرحله پیدا کنید:
.
بیایید حد دست راست را پیدا کنیم:
ایکس \u003d 0 باید برای شاخه تابعی یافت شود که شامل این نقطه باشد ، یعنی شاخه دوم. ما آنها را پیدا می کنیم:
همانطور که می بینید ، حد تابع و مقدار تابع در نقطه است ایکس \u003d 0 برابر است. بنابراین ، تابع در نقطه مداوم است ایکس = 0 .
نقطه ایکس \u003d 1 حد دست چپ را در این مرحله پیدا کنید:
بیایید حد دست راست را پیدا کنیم:
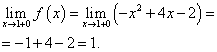
حد عملکرد و مقدار عملکرد در نقطه ایکس \u003d 1 باید برای شاخه تابعی یافت شود که شامل این نقطه باشد ، یعنی شاخه دوم. ما آنها را پیدا می کنیم:
.
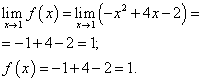حد عملکرد و مقدار عملکرد در نقطه ایکس \u003d 1 برابر است. بنابراین ، تابع در نقطه مداوم است ایکس = 1 .
نقطه ایکس \u003d 3 حد دست چپ را در این مرحله پیدا کنید:
بیایید حد دست راست را پیدا کنیم:
حد عملکرد و مقدار عملکرد در نقطه ایکس \u003d 3 باید برای شاخه تابعی یافت شود که شامل این نقطه باشد ، یعنی شاخه دوم. ما آنها را پیدا می کنیم:
.
حد عملکرد و مقدار عملکرد در نقطه ایکس \u003d 3 برابر است. بنابراین ، تابع در نقطه مداوم است ایکس = 3 .
نتیجه گیری اصلی: این تابع در هر نقطه مرزی پیوسته است.
خودتان تداوم عملکرد را در یک نقطه تنظیم کنید و سپس راه حل را ببینید
یک تغییر مداوم در یک تابع را می توان به عنوان یک تغییر تدریجی ، بدون پرش ، تعریف کرد که در آن یک تغییر کوچک در آرگومان منجر به یک تغییر کوچک در تابع می شود.
اجازه دهید این تغییر عملکرد مداوم را با یک مثال نشان دهیم.
بگذارید باری روی میز آویزان شود. تحت عمل این بار ، نخ کشیده می شود ، بنابراین فاصله است من وزن از نقطه تعلیق نخ تابعی از وزن وزن است متر ، یعنی من = f(متر) , متر≥0 .
اگر جرم بار را کمی تغییر دهیم ، فاصله را تغییر می دهیم من کمی تغییر: تغییرات کوچک متر تغییرات کوچک مطابقت دارد من ... با این حال ، اگر جرم بار نزدیک به مقاومت کششی نخ باشد ، افزایش جزئی وزن می تواند باعث شکستن نخ شود: فاصله من به طور ناگهانی افزایش می یابد و برابر با فاصله از نقطه تعلیق تا سطح میز می شود. نمودار عملکرد من = f(متر) در شکل نشان داده شده است. در سایت ، این نمودار یک خط مداوم (جامد) است و در یک نقطه قطع می شود. نتیجه یک نمودار با دو شاخه است. در همه نقاط به جز عملکرد من = f(متر) مداوم است ، و در نقطه آن یک ناپیوستگی است.
مطالعه یک تابع برای تداوم می تواند هم یک کار مستقل باشد و هم یکی از مراحل مطالعه کامل یک تابع و ساخت نمودار آن.
تداوم عملکرد در فاصله
اجازه دهید تابع بله = f(ایکس) در فاصله تعیین شده] آ, ب[و در هر نقطه از این فاصله مداوم است. سپس به آن مداوم در فاصله گفته می شود] آ, ب[. مفهوم تداوم یک تابع در فواصل فرم] - ∞ ، ب[ , ]آ، + ∞ [،] - ∞ ، + ∞ [. حالا اجازه دهید تابع بله = f(ایکس) در بخش تعریف شده است آ, ب] تفاوت بین فاصله و خط: نقاط انتهایی بازه در این بازه گنجانده نمی شوند و نقاط انتهایی خط در خط گنجانده می شوند. در اینجا باید به اصطلاح تداوم یک طرفه را ذکر کنیم: در نقطه آماندن در بخش [ آ, ب] ، ما فقط می توانیم از سمت راست و به نقطه نزدیک شویم ب - فقط در سمت چپ این تابع به صورت پیوسته بر روی بخش [ آ, ب] ، اگر در تمام نقاط داخلی این بخش مداوم باشد ، در نقطه درست پیوسته است آ و در نقطه چپ به طور مداوم است ب.
هر یک از توابع ابتدایی می تواند به عنوان نمونه ای از یک تابع مداوم عمل کند. هر تابع ابتدایی بر روی هر بخشی که بر روی آن تعریف شده است پیوسته است. به عنوان مثال ، توابع و در هر بخش مداوم هستند [ آ, ب] ، عملکرد به طور مداوم بر روی بخش [ 0 , ب] ، عملکرد بر روی هر قطعه ای که حاوی نقطه نباشد مداوم است آ = 2 .
مثال 4عملکرد را برای تداوم بررسی کنید.
تصمیم گیری شرط اول را بررسی می کنیم. این تابع در نقاط 3 و 3 تعریف نشده است. حداقل یکی از شرایط تداوم عملکرد در کل خط عدد برآورده نمی شود. بنابراین ، این عملکرد در فواصل مداوم است
.مثال 5 در چه مقدار از پارامتر تعیین کنید آ مداوم در سراسر زمینه های تعریف تابع 
تصمیم گیری
بیایید حد دست راست را در زیر پیدا کنیم:
.
بدیهی است که مقدار در نقطه ایکس \u003d 2 باید برابر باشد تبر :
آ = 1,5 .
مثال 6در چه مقادیری از پارامترها تعیین کنید آ و ب مداوم در سراسر زمینه های تعریف تابع 
تصمیم گیری
حد سمت چپ عملکرد را در نقطه پیدا کنید:
.
بنابراین ، مقدار در نقطه باید 1 باشد:
عملکرد چپ دست را در نقطه پیدا کنید:
بدیهی است که مقدار تابع در نقطه باید باشد:
پاسخ: این تابع در کل دامنه تعریف برای مداوم است آ = 1; ب = -3 .
خصوصیات اساسی توابع مداوم
ریاضیات با مطالعه ، قبل از هر چیز ، قوانین مختلف حرکت به مفهوم یک عملکرد مداوم رسیدند. فضا و زمان بی پایان هستند و اعتیاد مانند مسیرها s از زمان تی طبق قانون s = f(تی) ، مثالی از پیوسته را می دهد کارکرد f(تی) دمای آب گرم نیز به طور مداوم تغییر می کند ، همچنین یک عملکرد مداوم از زمان است: تی = f(تی) .
در تجزیه و تحلیل ریاضی ، برخی از خصوصیات ثابت شده است که توابع مداوم دارند. در اینجا مهمترین این خواص آورده شده است.
1. اگر یک تابع مداوم روی یک بازه مقادیر نشانه های مختلف را در انتهای بازه بگیرد ، در بعضی از نقاط این بخش مقداری برابر با صفر می گیرد. به طور رسمی ، این ویژگی در قضیه ای شناخته می شود که به عنوان اولین قضیه بولزانو-کوشی شناخته می شود.
2. عملکرد f(ایکس) ، به طور مداوم در فاصله [ آ, ب] ، تمام مقادیر میانی را بین مقادیر در نقاط انتهایی ، یعنی بین می گیرد f(آ) و f(ب) به طور رسمی ، این ویژگی در قضیه ای شناخته می شود که به عنوان قضیه دوم بولزانو-کوشی شناخته می شود.
اجازه دهید نکته آ مربوط به دامنه عملکرد است f (x) و هر ε -محله نقطه آ شامل غیر از آ نقاط دامنه عملکرد f (x)، یعنی نقطه آ نقطه محدودیت مجموعه است (ایکس)که در آن تابع f (x).
تعریف... تابع f (x) در نقطه پیوسته نامیده می شود آاگر تابع باشد f (x) در نقطه آ حد و این حد برابر با مقدار خاص است f (a) کارکرد f (x) در نقطه آ.
از این تعریف ما موارد زیر را داریم شرط تداوم عملکرد f (x) در نقطه آ :
از آن زمان می توانیم بنویسیم
بنابراین ، برای ادامه در نقطه آ نماد و نماد حد عملکرد f ویژگی های عملکرد را می توان مبادله کرد.
تعریف... تابع f (x) در قسمت راست (چپ) پیوسته نامیده می شود آاگر حد راست (چپ) این تابع در نقطه باشد آ وجود دارد و برابر با ارزش خصوصی است f (a) کارکرد f (x) در نقطه آ.
این واقعیت است که عملکرد f (x) مداوم در نقطه آ در سمت راست اینگونه نوشته شده است:
و تداوم عملکرد f (x) در نقطه آ در سمت چپ به صورت زیر نوشته شده است:
اظهار نظر... به نقاطی که تابعی خاصیت پیوستگی را ندارد نقاط ناپیوستگی این تابع گفته می شود.
قضیه... اجازه دهید توابع در همان مجموعه داده شوند f (x) و g (x)مداوم در نقطه آ... سپس توابع f (x) + g (x), f (x) -g (x), f (x) g (x) و f (x) / g (x) - مداوم در نقطه آ (در مورد خصوصی ، لازم است علاوه بر این گرم (الف) 0 پوند).
تداوم توابع اساسی
1) عملکرد قدرت y \u003d x n با طبیعی n در کل خط عدد پیوسته است.
ابتدا عملکرد را در نظر بگیرید f (x) \u003d x... طبق اولین تعریف از محدودیت یک تابع در نقطه آ هر دنباله ای را بگیرید (x n)همگرا شدن به آ، سپس دنباله مربوط به مقادیر توابع (f (x n) \u003d x n) همچنین به همگرایی خواهند کرد آ، یعنی 
، یعنی عملکرد f (x) \u003d x مداوم در هر نقطه از خط عدد.
اکنون تابع را در نظر بگیرید f (x) \u003d x nجایی که n یک عدد طبیعی است ، پس f (x) \u003d x x… x... اجازه دهید ما در حد مجاز عبور کنیم x → a، دریافت می کنیم ، یعنی عملکرد f (x) \u003d x n روی خط عدد پیوسته است.
2) عملکرد نمایی.
عملکرد نمایی y \u003d a x در a\u003e 1 یک تابع مداوم در هر نقطه از یک خط بی نهایت است.
عملکرد نمایی y \u003d a x در a\u003e 1 شرایط را برآورده می کند:
3) عملکرد لگاریتمی.
عملکرد لگاریتمی پیوسته است و در کل نیمه خط افزایش می یابد x\u003e 0 در a\u003e 1 مداوم است و در کل نیمه خط کاهش می یابد x\u003e 0 در 0
4) توابع هذلولی.
توابع زیر را توابع هذلولی می نامند:
از تعریف توابع هذلولی نتیجه می گیرد که کسینوس هایپربولیک ، سینوس هایپربولیک و مماس هذلولی در کل محور عددی تعریف می شوند ، و کتانژانت هذلولی در همه جای محور عددی به غیر از نقطه تعریف می شود x \u003d 0.
توابع هذلولی در هر نقطه از حوزه خود مداوم هستند (این امر از تداوم تابع نمایی و قضیه مربوط به عملیات حساب برمی آید).
5) عملکرد قدرت
تابع توان y \u003d x α \u003d a α log a x مداوم در هر نقطه از نیمه خط باز x\u003e 0.
6) توابع مثلثاتی.
کارکرد گناه x و cos x مداوم در هر نقطه ایکس خط مستقیم بی نهایت. تابع y \u003d tg x (kπ-π / 2 ، kπ + π / 2)و عملکرد y \u003d ctg x در هر یک از فواصل مداوم ((k-1) π ، kπ) (همه جا اینجا ک - هر عدد صحیح ، به عنوان مثال k \u003d 0 ، ± 1 ، ± 2 ، ...).
7) توابع مثلثاتی معکوس.
کارکرد y \u003d arcsin x و y \u003d آرکوس x مداوم در بخش [-1, 1] ... کارکرد y \u003d arctan x و y \u003d arctct x در یک خط بی نهایت مداوم هستند.
دو حد عالی
قضیه... محدودیت عملکرد (گناه x) / x در نقطه x \u003d 0 وجود دارد و برابر با یک است ، یعنی
این حد نامیده می شود اولین حد عالی.
شواهد و مدارک... چه زمانی 0
این نابرابری ها برای مقادیر نیز معتبر هستند ایکستأمین شرایط -π / 2 
... زیرا cos x یک تابع مداوم است ، بنابراین 
... بنابراین ، برای توابع cos x، 1 و در بعضی δ
-محله نقطه x \u003d 0 تمام شرایط قضیه ها راضی است. از این رو ، 
.
قضیه... محدودیت عملکرد 
در x → ∞ وجود دارد و برابر با عدد است ه:
این حد نامیده می شود دومین حد عالی.
اظهار نظر... همچنین این درست است که
تداوم یک عملکرد پیچیده
قضیه... اجازه دهید تابع x \u003d φ (t) مداوم در نقطه آو عملکرد y \u003d f (x) مداوم در نقطه b \u003d φ (a)... سپس عملکرد پیچیده y \u003d f [φ (t)] \u003d F (t) مداوم در نقطه آ.
بگذار x \u003d φ (t) و y \u003d f (x) ساده ترین توابع ابتدایی و مجموعه مقادیر هستند (ایکس) کارکرد x \u003d φ (t) دامنه عملکرد است y \u003d f (x)... همانطور که می دانیم ، توابع ابتدایی در هر نقطه از حوزه وظیفه مداوم هستند. بنابراین ، طبق قضیه قبلی ، تابع پیچیده است y \u003d f (φ (t))، یعنی برهم نهی دو عملکرد ابتدایی پیوسته است. به عنوان مثال ، عملکرد در هر نقطه مداوم است x ≠ 0به عنوان تابعی پیچیده از دو عملکرد اساسی x \u003d t -1 و y \u003d گناه x... همچنین عملکرد y \u003d ln sin x مداوم در هر نقطه از فواصل (2kπ ، (2k + 1) π), k ∈ Z (sin x\u003e 0).
تداوم یک تابع در یک نقطه.
تابعی که در محله ای از بعضی نقاط تعریف شده باشد ، فراخوانی می شود مداوم در نقطهاگر حد تابع و مقدار آن در این نقطه برابر باشد ، به عنوان مثال
همان واقعیت را می توان متفاوت نوشت:
اگر تابعی در بعضی از محله های یک نقطه تعریف شود ، اما در خود نقطه مداوم نباشد ، آنرا فراخوانی می کنیم ناپیوسته تابع ، و نقطه یک نقطه شکست است.
مثالی از یک تابع مداوم:
0 x 0 -D x 0 x 0 + D x
مثالی از یک تابع ناپیوسته:
اگر برای هر عدد مثبت چنان عددی وجود داشته باشد که برای هر شرط ارضاying کننده ای وجود داشته باشد: یک نابرابری درست است.
تابع فراخوانی می شود مداوم در یک نقطه اگر افزایش عملکرد در نقطه بی نهایت کم باشد.
بی نهایت در کجاست
خصوصیات توابع پیوسته.
1) مجموع ، تفاوت و حاصل از توابع مداوم در یک نقطه تابعی است که در یک نقطه مداوم است.
2) ضریب دو تابع پیوسته یک تابع مداوم است به شرطی که در نقطه برابر با صفر نباشد.
3) برهم زدن توابع پیوسته یک تابع مداوم است.
این ویژگی را می توان به صورت زیر نوشت:
اگر در یک نقطه توابع پیوسته باشند ، در این مرحله نیز عملکرد تابعی مداوم است.
خصوصیات فوق به راحتی توسط اثبات می شود
با استفاده از قضیه های حد.
تداوم برخی از توابع ابتدایی.
1. عملکرد ، یک عملکرد مداوم در کل دامنه است.
2. عملکرد منطقی برای همه مقادیر پیوسته است ، به جز مقادیری که مخرج در آنها از بین می رود. بنابراین ، تابعی از این نوع در کل دامنه مداوم است.
3. توابع مثلثاتی و در حوزه تعریف خود پیوسته هستند.
اجازه دهید ویژگی 3 را برای عملکرد ثابت کنیم.
بیایید افزایش تابع یا پس از تغییر را بنویسیم:
در واقع ، یک محدودیت از محصول دو عملکرد وجود دارد و. در این حالت ، تابع کسینوس یک تابع محدود در ، و از آن زمان است حد عملکرد سینوسی ، پس از آن در کمترین حد است.
بنابراین ، محصولی از یک تابع محدود شده توسط یک عملکرد نامحدود وجود دارد ، بنابراین ، این محصول ، یعنی عملکرد بی نهایت کم است. مطابق با تعاریف فوق ، یک تابع یک تابع مداوم برای هر مقداری از حوزه تعریف است ، از آنجا که افزایش آن در این مرحله یک مقدار بینهایت کم است.
نقاط شکست و طبقه بندی آنها.
برخی از عملکردها را در نظر بگیرید که در مجاورت یک نقطه مداوم است ، به استثنای احتمالاً خود این نقطه. از تعریف یک نقطه ناپیوستگی یک تابع ، نتیجه می شود که اگر تابع در این نقطه تعریف نشده باشد یا در آن مداوم نباشد ، یک نقطه ناپیوستگی است.
همچنین باید توجه داشت که تداوم یک تابع می تواند یک طرفه باشد. بگذارید این را به شرح زیر توضیح دهیم.
اگر حد یک طرفه باشد (نگاه کنید به بالا) ، آنگاه عملکرد را پیوسته می نامند.
نقطه نامیده می شود نقطه شکستتابع اگر در یک نقطه تعریف نشده باشد یا در آن نقطه مداوم نباشد.
نقطه نامیده می شود نقطه شکست از نوع 1، اگر در این مرحله تابع محدود باشد ، اما با یکدیگر برابر نیست ، حد چپ و راست:
برای تحقق شرایط این تعریف ، لازم نیست تابع در یک نقطه تعریف شود ، فقط کافی است که در سمت چپ و راست آن تعریف شود.
از تعریف ، می توان نتیجه گرفت که در نقطه ناپیوستگی نوع 1 ، این تابع می تواند فقط یک جهش محدود داشته باشد. در برخی موارد خاص ، گاهی اوقات نقطه شکست از نوع 1 نامیده می شود قابل جابجایینقطه انفصال ، اما در اینجا بیشتر در این مورد صحبت خواهیم کرد.
نقطه نامیده می شود نقطه شکست از نوع 2اگر در این مرحله تابع حداقل یکی از حد یک طرفه را نداشته باشد ، یا حداقل یکی از آنها بی نهایت باشد.
مثال 1 ... تابع دیریشله (Dirichlet Peter Gustav (1805-1859) - ریاضیدان آلمانی ، عضو متناظر آکادمی علوم سن پترزبورگ 1837)
در هر نقطه x 0 پیوسته نیست.
مثال 2 ... از آن زمان ، این تابع از نوع 2 دارای نقطه ناپیوستگی است ...
مثال 3 .
تابع در یک نقطه تعریف نشده است ، اما دارای یک حد محدود در آن است ، به عنوان مثال در نقطه عملکرد ، نوع ناپیوستگی از نوع 1 است. این یک نقطه شکست یکبار مصرف است زیرا اگر عملکرد را دوباره تعریف کنیم:
نمودار این عملکرد:
مثال 4 .
این عملکرد با علامت - نیز نشان داده می شود. عملکرد در نقطه تعریف نشده است. زیرا محدودیت های چپ و راست تابع متفاوت است ، سپس نقطه شکست از نوع اول است. اگر تعریف یک تابع را در یک نقطه با قرار دادن گسترش دهیم ، آنگاه تابع در سمت راست پیوسته خواهد بود ، اگر قرار دهیم ، تابع در سمت چپ پیوسته خواهد بود ، اگر برابر هر عددی غیر از 1 یا -1 قرار دهیم ، در این صورت تابع نه در سمت چپ و نه در سمت راست ادامه خواهد داشت ، اما با این وجود ، در همه موارد ، از نوع 1 استراحت خواهد داشت. در این مثال ، نقطه شکست نوع 1 قابل جابجایی نیست.
بنابراین ، برای اینکه نقطه ناپیوستگی نوع 1 قابل جابجایی باشد ، لازم است که محدوده های یک طرفه در سمت راست و چپ محدود و مساوی باشند ، و عملکرد در این نقطه تعریف نشده است.
2.2. تداوم یک تابع در یک فاصله و روی یک بخش.
تابع فراخوانی می شود مداوم در فاصله (بخش)اگر در هر نقطه از فاصله (قطعه) مداوم باشد.
در این حالت ، تداوم عملکرد در انتهای قطعه یا بازه مورد نیاز نیست ، فقط پیوستگی یک طرفه در انتهای قطعه یا بازه مورد نیاز است.
خصوصیات توابع که روی یک بخش مداوم هستند.
املاک 1. (اولین قضیه Weierstrass (Weierstrass Karl (1897-1815) - ریاضیدان آلمانی)). تابعی که به طور مداوم بر روی یک بخش باشد به این بخش محدود می شود ، یعنی در بخش شرط زیر برآورده شده است:
اثبات این ویژگی بر این اساس استوار است که تابعی که در یک نقطه مداوم باشد در بعضی از محله های آن محدود شده است و اگر یک قطعه را به تعداد نامحدودی از بخشهایی تقسیم کنیم که به یک نقطه "منقبض" می شوند ، در آن صورت برخی از محله های نقطه شکل می گیرند.
خاصیت 2. تابعی که روی یک قطعه مداوم باشد ، بزرگترین و کوچکترین مقادیر را روی خود می گیرد.
آنهایی که مقادیر وجود دارد و از این قبیل ،
بیایید توجه داشته باشیم. که تابع می تواند این بزرگترین و کوچکترین مقادیر را در یک بازه زمانی و چندین بار بگیرد (به عنوان مثال -).
تفاوت بین بزرگترین و کوچکترین مقادیر یک تابع را بر روی یک بخش می نامند تردیدتوابع روی یک بخش
املاک 3. (قضیه دوم بولزانو - کوشی). تابعی که بر روی یک بخش مداوم باشد ، تمام مقادیر بین دو مقدار دلخواه را بر روی این بخش می گیرد.
4. اگر یک تابع در یک نقطه مداوم باشد ، در آن صورت محله ای از نقطه وجود دارد که تابع علامت خود را حفظ می کند.
املاک 5. (قضیه اول بولزانو (1848-1781) - کوشی). اگر این تابع روی یک قطعه مداوم باشد و در انتهای قسمت دارای نشانه های مخالف باشد ، یک نقطه در داخل این بخش وجود دارد ، کجا. و نزدیک به صفر هستند.
در نقطه عملکرد تداوم دارد در نقطه نقطه ناپیوستگی نوع 1 است
سخنرانی 4
تداوم توابع
1. تداوم یک تابع در یک نقطه
تعریف 1اجازه دهید تابع بله=f(ایکس) در نقطه تعریف شده است ایکس 0 و در بعضی از محله های این نقطه تابع بله=f(ایکس) نامیده میشود پیوسته در نقطه x 0 اگر محدودیتی از تابع در این نقطه وجود داشته باشد و برابر با مقدار تابع در این نقطه باشد ، یعنی
بنابراین ، شرایط تداوم برای عملکرد بله=f(ایکس) در نقطه ایکس 0 این است که:
زیرا 
، سپس برابری (32) را می توان در فرم نوشت
(33)
این بدان معنی است که برای پیدا کردن حد یک تابع مداومf(ایکس) می توانید در علامت تابع به حد مجاز بروید ، یعنی به عملکرد f(ایکس) به جای استدلال ایکس حد خود را جایگزین کنید ایکس 0 .
گناه گناه ایکس\u003d گناه (لیم ایکس);
lim arctg ایکس\u003d arctg (لیمو ایکس); (34)
بسیار کم است ایکس\u003d ورود به سیستم (lim ایکس).
وظیفهحد را پیدا کنید: 1) 
;
2)
.
اجازه دهید تعریفی از تداوم یک تابع ، بر اساس مفهوم آرگومان و افزایش عملکرد ارائه دهیم.
زیرا شرایط 
و 
همان هستند (شکل 4) ، سپس برابری (32) شکل می گیرد:
یا 
.
تعریف 2 تابع بله=f(ایکس) نامیده میشود پیوسته در نقطه x 0 , اگر در نقطه تعریف شود ایکس 0 و همسایگی آن ، و یک افزایش بی نهایت کوچک از آرگومان مربوط به یک افزایش بی نهایت از تابع است.
وظیفه پیوستگی یک تابع را بررسی کنید بله=2ایکس 2 1.
ویژگی های توابع که در یک نقطه مداوم هستند
1. اگر توابع f(ایکس) و φ
(ایکس) در نقطه مداوم هستند ایکس 0 ، سپس جمع آنها 
، ترکیب بندی 
و خصوصی 
(با توجه به اینکه 
) توابع پیوسته در نقطه هستند ایکس 0 .
2. اگر تابع در=f(ایکس) در نقطه مداوم است ایکس 0 و f(ایکس 0)\u003e 0 ، پس محله ای از نقطه وجود دارد ایکس 0 که در آن f(ایکس)>0.
3. اگر تابع در=f(تو) در نقطه u 0 پیوسته است ، و تابع u \u003d φ (ایکس) در نقطه مداوم است تو 0 \u003d φ (ایکس 0 ) ، سپس تابع پیچیده است بله=f[φ (ایکس)] در نقطه مداوم است ایکس 0 .
2. تداوم تابع در فاصله و بر روی بخش
کارکرد بله=f(ایکس) نامیده میشود مداوم در فاصله (آ; ب) اگر در هر نقطه از این فاصله مداوم باشد.
کارکرد بله=f(ایکس) نامیده میشود مداوم بر روی بخش
[آ;
ب] اگر در فاصله مداوم باشد ( آ;
ب) ، و در نقطه ایکس=و در سمت راست پیوسته است (یعنی 
) ، و در نقطه ایکس=ب در سمت چپ پیوسته است (یعنی 
).
3. نقاط شکست یک تابع و طبقه بندی آنها
نقاطی که پیوستگی عملکرد شکسته می شود نقاط شکست این عملکرد
اگر یک ایکس=ایکس 0 نقطه ناپیوستگی عملکرد بله=f(ایکس) ، حداقل یکی از شرایط تعریف اول تداوم یک تابع در آن راضی نیست.
مثال.
1.
. 2.
3)
4)
.
▼ نقطه شکست ایکس 0 نقطه ناپیوستگی نامیده می شود نوع اول کارکرد بله=f(ایکس) ، اگر در این مرحله محدودیت های محدودی از تابع در سمت چپ و راست (محدوده های یک طرفه) وجود داشته باشد ، یعنی 
و 
... که در آن:
مقدار | آ 1 -آ 2 | نامیده می شود عملکرد پرش در نقطه شکست نوع اول. ▲
▼ نقطه شکست ایکس 0 نقطه ناپیوستگی نامیده می شود نوع دوم کارکرد بله=f(ایکس) اگر حداقل یکی از حد یک طرفه (چپ یا راست) وجود نداشته باشد یا برابر با بی نهایت باشد. ▲
وظیفه نقاط شکست را پیدا کنید و نوع آنها را برای توابع پیدا کنید:
1)
;
2)
.
4. قضیه های اساسی در مورد توابع مداوم
قضیه های تداوم توابع مستقیماً از قضیه های مربوطه در مورد حدود پیروی می کنند.
قضیه 1 حاصل جمع ، ضریب و ضریب دو تابع پیوسته یک تابع پیوسته است (برای ضریب ، به جز مقادیر آرگومان که تقسیم کننده در آن صفر نیست).
قضیه 2 اجازه دهید توابع تو=φ (ایکس) در نقطه مداوم است ایکس 0 ، و عملکرد بله=f(تو) در نقطه مداوم است تو=φ (ایکس 0 ) سپس عملکرد پیچیده f(φ (ایکس)) ، متشکل از توابع مداوم ، در نقطه مداوم است ایکس 0 .
قضیه 3. اگر تابع بله=f(ایکس) مداوم و کاملاً یکنواخت در [ آ; ب] محور اوه، سپس عملکرد معکوس در=φ (ایکس) همچنین در بخش مربوطه پیوسته و یکنواخت است [ ج;د] محور OU
هر تابع ابتدایی در هر نقطه ای که تعریف شود پیوسته است.
5. خصوصیات توابع به طور مداوم در یک بخش
قضیه Weierstrass. اگر یک تابع روی یک قطعه مداوم باشد ، پس از آن به بزرگترین و کوچکترین مقادیر خود روی این قطعه می رسد.
نتیجه. اگر یک تابع در یک بخش مداوم باشد ، پس به بخش محدود می شود.
قضیه بولزانو کوشی.اگر تابع بله=f(ایکس) به صورت مداوم بر روی بخش [ آ;
ب] و مقادیر نابرابر را در انتهای خود می گیرد f(آ)=آ و f(ب)=ب,
سپس هر تعداد باشد از جانببین و و که در،یک نکته وجود دارد
به طوری که f(ج)=ج.
از نظر هندسی قضیه واضح است. برای هر شماره از جانببین و و که در، یک نقطه در داخل این بخش وجود دارد به طوری که f(از جانب)=ج... سر راست در=از جانب نمودار تابع را حداقل یک نقطه قطع می کند.
نتیجه. اگر تابع بله=f(ایکس) به صورت مداوم بر روی بخش [ آ; ب] و مقادیر نشانه های مختلف را در انتهای آن گرفته و سپس در داخل بخش قرار می دهد [ آ; ب] حداقل یک نکته وجود دارد از جانبکه در آن تابع بله=f(ایکس) ناپدید می شود: f(ج)=0.
هندسیمعنای قضیه: اگر نمودار یک تابع پیوسته از یک طرف محور عبور کند اوه به دیگری ، سپس از محور عبور می کند اوه.
بارگذاری ...