În această lecție, vom învăța să stabilim continuitatea unei funcții. Vom face acest lucru folosind limite și unilaterale - dreapta și stânga, care nu sunt deloc înfricoșătoare, în ciuda faptului că sunt scrise ca și.
Dar care este continuitatea unei funcții în general? Până când ajungem la o definiție strictă, este cel mai ușor să ne imaginăm o linie care poate fi trasată fără a ridica creionul de pe hârtie. Dacă se trasează o astfel de linie, atunci este continuă. Această linie este graficul unei funcții continue.
Grafic, o funcție este continuă într-un punct, dacă graficul său nu se „rupe” în acel punct. Graficul unei astfel de funcții continue - 
prezentat în figura de mai jos.
Determinarea continuității unei funcții prin limită. Funcția este continuă la un moment dat dacă sunt îndeplinite trei condiții:
1. Funcția este definită într-un punct.
Dacă cel puțin una dintre condițiile enumerate nu este îndeplinită, funcția nu este continuă la punctul respectiv. În acest caz, ei spun că funcția are o pauză, iar punctele de pe graficul în care graficul este întrerupt se numesc punctele de pauză ale funcției. Graficul unei astfel de funcții, care este discontinuu la punctul x \u003d 2, este prezentat în figura de mai jos.
Exemplul 1.Funcţie f(x) este definit astfel:
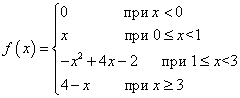
Această funcție va fi continuă la fiecare dintre punctele limită ale ramurilor sale, adică la puncte x = 0 , x = 1 , x = 3 ?
Decizie. Verificăm toate cele trei condiții pentru continuitatea funcției la fiecare punct de graniță. Prima condiție este îndeplinită, deoarece faptul că funcție definită la fiecare dintre punctele limită rezultă din definiția funcției. Rămâne să verificăm celelalte două condiții.
Punct x \u003d 0. Găsiți limita la stânga în acest moment:
.
Să găsim limita la dreapta:
x \u003d 0 trebuie găsit pentru ramura funcției care include acest punct, adică a doua ramură. Le găsim:
După cum puteți vedea, limita funcției și valoarea funcției la punctul respectiv x \u003d 0 sunt egale. Prin urmare, funcția este continuă la punctul respectiv x = 0 .
Punct x \u003d 1. Găsiți limita la stânga în acest moment:
Să găsim limita la dreapta:
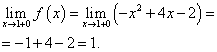
Limita funcției și valoarea funcției la punctul x \u003d 1 trebuie găsit pentru ramura funcției care include acest punct, adică a doua ramură. Le găsim:
.
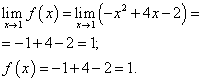Limita funcției și valoarea funcției la punctul x \u003d 1 sunt egale. Prin urmare, funcția este continuă la punctul respectiv x = 1 .
Punct x \u003d 3. Găsiți limita la stânga în acest moment:
Să găsim limita la dreapta:
Limita funcției și valoarea funcției la punctul x \u003d 3 trebuie găsit pentru ramura funcției care include acest punct, adică a doua ramură. Le găsim:
.
Limita funcției și valoarea funcției la punctul x \u003d 3 sunt egale. Prin urmare, funcția este continuă la punctul respectiv x = 3 .
Concluzia principală: această funcție este continuă la fiecare punct limită.
Setați continuitatea funcției într-un anumit punct și apoi vedeți soluția
O schimbare continuă într-o funcție poate fi definită ca o schimbare treptată, fără salturi, în care o mică modificare a argumentului duce la o mică modificare a funcției.
Să ilustrăm această schimbare continuă a funcției cu un exemplu.
Lasă o încărcătură să atârne deasupra mesei. Sub acțiunea acestei sarcini, firul este întins, deci distanța l greutatea de la punctul de suspensie al filetului este o funcție a greutății greutății m , adică l = f(m) , m≥0 .
Dacă schimbăm ușor greutatea sarcinii, atunci distanța l mica schimbare: mici schimbari m mici modificări corespund l ... Cu toate acestea, dacă masa sarcinii este aproape de rezistența la tracțiune a firului, atunci o ușoară creștere a greutății sarcinii poate provoca ruperea firului: distanța l va crește brusc și va deveni egal cu distanța de la punctul de suspensie la suprafața mesei. Graficul funcțional l = f(m) prezentată în figură. Pe site, acest grafic este o linie continuă (continuă) și într-un punct este întrerupt. Rezultatul este un grafic cu două ramuri. În toate punctele, cu excepția funcției l = f(m) este continuu, iar la momentul respectiv are o discontinuitate.
Studiul unei funcții pentru continuitate poate fi atât o sarcină independentă, cât și una dintre etapele unui studiu complet al unei funcții și construirea graficului acesteia.
Continuitatea funcției pe interval
Să funcția y = f(x) definit în interval] a, b[și este continuu în fiecare punct al acestui interval. Apoi se numește continuu în interval] a, b[. Conceptul de continuitate a unei funcții pe intervale de formă] - ∞, b[ , ]a, + ∞ [,] - ∞, + ∞ [. Acum lăsați funcția y = f(x) este definit pe segmentul [ a, b]. Diferența dintre interval și linie: punctele finale ale intervalului nu sunt incluse în interval, iar punctele finale ale liniei sunt incluse în linie. Aici ar trebui să menționăm așa-numita continuitate unilaterală: la punct arămânând pe segment [ a, b], nu ne putem apropia decât de la dreapta și la obiect b - doar în stânga. Funcția se numește continuă pe segmentul [ a, b], dacă este continuu la toate punctele interioare ale acestui segment, dreapta-continuu la punctul a și este continuu în stânga la punctul respectiv b.
Oricare dintre funcțiile elementare poate servi ca exemplu de funcție continuă. Fiecare funcție elementară este continuă pe orice segment pe care este definită. De exemplu, funcțiile și sunt continue pe orice segment [ a, b], funcția este continuă pe segmentul [ 0 , b], funcția este continuă pe orice segment care nu conține punctul a = 2 .
Exemplul 4.Examinați funcția pentru continuitate.
Decizie. Verificăm prima condiție. Funcția nu este definită la punctele - 3 și 3. Cel puțin una dintre condițiile pentru continuitatea funcției pe întreaga linie numerică nu este îndeplinită. Prin urmare, această funcție este continuă pe intervale
.Exemplul 5. Determinați la ce valoare a parametrului a continuu pe tot parcursul domenii de definire funcţie 
Decizie.
Să găsim limita la dreapta la:
.
Evident, valoarea la punctul respectiv x \u003d 2 ar trebui să fie egală topor :
a = 1,5 .
Exemplul 6.Determinați la ce valori ale parametrilor a și b continuu pe tot parcursul domenii de definire funcţie 
Decizie.
Găsiți limita din stânga a funcției la punctul:
.
Prin urmare, valoarea la punctul trebuie să fie 1:
Găsiți funcția stângaci la punctul:
Evident, valoarea funcției la punctul respectiv trebuie să fie egală cu:
Răspuns: funcția este continuă pe întregul domeniu al definiției la a = 1; b = -3 .
Proprietățile de bază ale funcțiilor continue
Matematica a ajuns la conceptul de funcție continuă prin studierea, în primul rând, a diferitelor legi ale mișcării. Spațiul și timpul sunt nesfârșite și dependența, precum cărările s din timp t prin lege s = f(t) , dă un exemplu de continuu funcții f(t). Temperatura apei încălzite se schimbă continuu, de asemenea, este o funcție continuă a timpului: T = f(t) .
În analiza matematică, s-a dovedit că unele proprietăți au funcții continue. Iată cele mai importante dintre aceste proprietăți.
1. Dacă o funcție continuă pe un interval ia valori de semne diferite la capetele intervalului, atunci la un moment dat al acestui segment ia o valoare egală cu zero. Mai formal, această proprietate este dată într-o teoremă cunoscută sub numele de prima teoremă Bolzano-Cauchy.
2. Funcția f(x), continuu pe intervalul [ a, b], ia toate valorile intermediare între valorile de la punctele finale, adică între f(a) și f(b). Mai formal, această proprietate este dată într-o teoremă cunoscută sub numele de a doua teoremă Bolzano-Cauchy.
Lasă punctul a aparține sferei funcției f (x) și orice ε -vecinătatea punctului a conține altele decât a funcție puncte domeniu f (x), adică punct a este punctul limită al setului (X)pe care funcția f (x).
Definiție... Funcţie f (x) se numește continuu la punct adacă funcție f (x) are la punct a limită și această limită este egală cu valoarea particulară f (a) funcții f (x) la punct a.
Din această definiție avem următoarele condiția de continuitate a funcției f (x) la punct a :
De atunci putem scrie
Prin urmare, pentru continuu la punct a simbol limita funcției și simbol f caracteristicile funcției pot fi schimbate.
Definiție... Funcţie f (x) se numește continuu în dreapta (stânga) în punct adacă limita dreaptă (stânga) a acestei funcții la punct a există și este egal cu valoarea privată f (a) funcții f (x) la punct a.
Faptul că funcția f (x) continuu la punct a în dreapta este scris astfel:
Și continuitatea funcției f (x) la punct a în stânga este scris:
cometariu... Punctele în care o funcție nu are proprietatea continuității se numesc puncte de discontinuitate ale acestei funcții.
Teorema... Funcțiile să fie date pe același set f (x) și g (x)continuu la punct a... Apoi funcțiile f (x) + g (x), f (x) -g (x), f (x) g (x) și f (x) / g (x) - continuu la punct a (în cazul unui privat, trebuie să solicitați suplimentar g (a) ≠ 0).
Continuitatea funcțiilor elementare de bază
1) Funcția de alimentare y \u003d x n cu natural n este continuu pe linia numerelor întregi.
În primul rând, ia în considerare funcția f (x) \u003d x... Conform primei definiții a limitei unei funcții la punct a ia orice secvență (x n)convergând către a, apoi secvența de valori corespunzătoare a funcțiilor (f (x n) \u003d x n) va converge și în a, adică 
, adică funcția f (x) \u003d x continuu în orice punct de pe linia numerică.
Acum ia în considerare funcția f (x) \u003d x nUnde n - numar naturalatunci f (x) \u003d x x… x... Să trecem la limită la x → a, obținem, adică funcția f (x) \u003d x n este continuu pe linia numerică.
2) Funcția exponențială.
Functie exponentiala y \u003d a x la a\u003e 1 este o funcție continuă în orice punct al unei linii infinite.
Functie exponentiala y \u003d a x la a\u003e 1 îndeplinește condițiile:
3) Funcția logaritmică.
Funcția logaritmică este continuă și crește de-a lungul întregii jumătăți de linie x\u003e 0 la a\u003e 1 și este continuu și scade pe toată jumătatea liniei x\u003e 0 la 0
4) Funcții hiperbolice.
Următoarele funcții se numesc funcții hiperbolice:
Din definiția funcțiilor hiperbolice rezultă că cosinusul hiperbolic, sinusul hiperbolic și tangenta hiperbolică sunt definite pe întreaga axă numerică, iar cotangenta hiperbolică este definită peste tot pe axa numărului, cu excepția punctului x \u003d 0.
Funcțiile hiperbolice sunt continue în fiecare punct al domeniului lor (aceasta rezultă din continuitatea funcției exponențiale și teorema operațiunilor aritmetice).
5) Funcția de alimentare
Funcția de alimentare y \u003d x α \u003d a α log a x continuu în fiecare punct al jumătății deschise x\u003e 0.
6) Funcții trigonometrice.
Funcții păcat x și cos x continuu în fiecare punct x linie dreaptă infinită. Funcţie y \u003d tg x (kπ-π / 2, kπ + π / 2)și funcția y \u003d ctg x continuu pe fiecare dintre intervale ((k-1) π, kπ) (peste tot aici k - orice număr întreg, adică k \u003d 0, ± 1, ± 2, ...).
7) Funcții trigonometrice inverse.
Funcții y \u003d arcsin x și y \u003d arccos x continuu pe segment [-1, 1] ... Funcții y \u003d arctan x și y \u003d arcctg x sunt continue pe o linie infinită.
Două limite minunate
Teorema... Limita funcției (sin x) / x la punct x \u003d 0 există și este egal cu unul, adică
Această limită se numește prima limită minunată.
Dovezi... Când 0
Aceste inegalități sunt valabile și pentru valori xsatisfacerea condițiilor -π / 2 
... pentru că cos x este o funcție continuă, atunci 
... Astfel, pentru funcții cos x, 1 și în unele δ
-vecinătatea punctului x \u003d 0 toate condițiile teoremelor sunt îndeplinite. Prin urmare, 
.
Teorema... Limita funcției 
la x → ∞ există și este egal cu numărul e:
Această limită se numește a doua limită minunată.
cometariu... De asemenea, este adevărat că
Continuitatea unei funcții complexe
Teorema... Să funcția x \u003d φ (t) continuu la punct ași funcția y \u003d f (x) continuu la punct b \u003d φ (a)... Apoi funcția complexă y \u003d f [φ (t)] \u003d F (t) continuu la punct a.
Lasa x \u003d φ (t) și y \u003d f (x) sunt cele mai simple funcții elementare și setul de valori (X) funcții x \u003d φ (t) este scopul funcției y \u003d f (x)... După cum știm, funcțiile elementare sunt continue în fiecare punct al domeniului sarcinii. Prin urmare, conform teoremei anterioare, funcția complexă y \u003d f (φ (t)), adică suprapunerea a două funcții elementare este continuă. De exemplu, funcția este continuă în orice punct x ≠ 0ca o funcție complexă a două funcții elementare x \u003d t -1 și y \u003d sin x... De asemenea, funcția y \u003d ln sin x continuu la orice punct de intervale (2kπ, (2k + 1) π), k ∈ Z (sin x\u003e 0).
Continuitatea unei funcții într-un punct.
O funcție definită într-un vecinătate de un anumit punct este numită continuu la punctdacă limita funcției și valoarea acesteia în acest moment sunt egale, adică
Același fapt poate fi scris diferit:
Dacă o funcție este definită într-un vecinătate a unui punct, dar nu este continuă la punctul în sine, atunci se numește discontinuu funcție, iar punctul este un punct de rupere.
Un exemplu de funcție continuă:
0 x 0 -D x 0 x 0 + D x
Un exemplu de funcție discontinuă:
O funcție se numește continuă într-un punct dacă pentru orice număr pozitiv există un astfel de număr încât pentru orice care îndeplinește condiția: inegalitatea este adevărată.
Funcția se numește continuu într-un punct dacă creșterea funcției în punct este infinitesimală.
unde este infinitesimal la.
Proprietățile funcțiilor continue.
1) suma, diferența și produsul funcțiilor continue într-un punct este o funcție care este continuă într-un punct;
2) coeficientul a două funcții continue este o funcție continuă cu condiția să nu fie egal cu zero în punct;
3) suprapunerea funcțiilor continue este o funcție continuă.
Această proprietate poate fi scrisă după cum urmează:
Dacă sunt funcții continue într-un punct, atunci funcția este și o funcție continuă în acest punct.
Proprietățile de mai sus pot fi ușor dovedite de
folosind teoreme de limită.
Continuitatea unor funcții elementare.
1. Funcție, - funcție continuă pe întregul domeniu.
2. Funcția rațională este continuă pentru toate valorile, cu excepția celor la care numitorul dispare. Astfel, o funcție de acest tip este continuă pe întregul domeniu.
3. Funcțiile trigonometrice și sunt continue pe domeniul lor de definiție.
Să dovedim proprietatea 3 pentru funcție.
Să scriem creșterea funcției sau după transformare:
Într-adevăr, există o limită a produsului a două funcții și. În acest caz, funcția cosinusului este o funcție mărginită la și de atunci limita funcției sinusoidale, atunci este infinitesimală la.
Astfel, există un produs al unei funcții mărginite de una infinitesimală, prin urmare, acest produs, adică funcția este infinitesimală. În conformitate cu definițiile de mai sus, o funcție este o funcție continuă pentru orice valoare din domeniul definiției, deoarece creșterea sa în acest moment este o valoare infinit de mică.
Puncte de întrerupere și clasificarea lor.
Luați în considerare o funcție continuă în vecinătatea unui punct, cu posibila excepție a acestui punct în sine. Din definiția unui punct de discontinuitate al unei funcții, rezultă că este un punct de discontinuitate dacă funcția nu este definită în acest moment sau nu este continuă la aceasta.
De asemenea, trebuie remarcat faptul că continuitatea unei funcții poate fi unidirecțională. Să explicăm acest lucru după cum urmează.
Dacă limita este unilaterală (vezi mai sus), atunci funcția se numește dreapta-continuă.
Ideea se numește punct de ruperefuncție dacă nu este definită într-un punct sau nu este continuă în acel punct.
Ideea se numește punctul de rupere de primul fel, dacă în acest moment funcția are limite finite, dar nu egale între ele, stânga și dreapta:
Pentru a îndeplini condițiile acestei definiții, nu este necesară definirea funcției la un moment dat, este suficient ca aceasta să fie definită la stânga și la dreapta acesteia.
Din definiție, putem concluziona că la punctul de discontinuitate de primul fel, funcția poate avea doar un salt finit. În unele cazuri speciale, se numește uneori punctul de pauză de primul fel amovibilpunct de întrerupere, dar vom vorbi mai multe despre acest lucru mai jos.
Ideea se numește punctul de rupere de tipul 2dacă în acest moment funcția nu are cel puțin una dintre limitele unilaterale sau cel puțin una dintre ele este infinită.
Exemplul 1 ... Funcția Dirichlet (Dirichlet Peter Gustav (1805-1859) - matematician german, membru corespondent al Academiei de Științe din Sankt Petersburg 1837)
nu este continuu în niciun punct x 0.
Exemplul 2 ... Funcția are un punct de discontinuitate de tipul 2 la punctul, deoarece ...
Exemplul 3 .
Funcția nu este definită într-un punct, ci are o limită finită, adică la punctul funcția are un punct de discontinuitate de primul fel. Acesta este un punct de pauză de unică folosință deoarece dacă redefinim funcția:
Graficul acestei funcții:
Exemplul 4 .
Această funcție este indicată și de - semn. Funcția nu este definită la punctul respectiv. pentru că limitele stânga și dreapta ale funcției sunt diferite, atunci punctul de rupere este de primul fel. Dacă extindem definiția unei funcții într-un punct prin punere, atunci funcția va fi continuă în dreapta, dacă punem, atunci funcția va fi continuă în stânga, dacă punem egal cu orice alt număr decât 1 sau - 1, atunci funcția nu va fi continuă nici în stânga, nici în dreapta, dar în toate cazurile, totuși, va avea o pauză de primul fel la punctul respectiv. În acest exemplu, punctul de întrerupere de primul fel nu este eliminabil.
Astfel, pentru ca punctul de discontinuitate de primul tip să fie amovibil, este necesar ca limitele unilaterale din dreapta și stânga să fie finite și egale, iar funcția ar fi nedefinită în acest moment.
2.2. Continuitatea unei funcții pe un interval și pe un segment.
Funcția se numește continuu pe un interval (segment)dacă este continuă în orice punct al intervalului (segmentului).
În acest caz, continuitatea funcției la capetele segmentului sau intervalului nu este necesară, este necesară doar continuitate unilaterală la capetele segmentului sau intervalului.
Proprietățile funcțiilor care sunt continue pe un segment.
Proprietatea 1. (Prima teoremă a lui Weierstrass (Weierstrass Karl (1815-1897) - matematician german)). O funcție care este continuă pe un segment este delimitată pe acest segment, adică pe segment se îndeplinește următoarea condiție:
Dovada acestei proprietăți se bazează pe faptul că o funcție care este continuă într-un punct este mărginită într-o parte din vecinătatea ei și dacă împărțim un segment într-un număr infinit de segmente care „se contractă” într-un punct, atunci unele vecinătăți a punctului se formează.
Proprietatea 2. O funcție continuă pe un segment ia cele mai mari și mai mici valori pe ea.
Acestea. există valori și astfel încât ,, și:
Să observăm. că funcția poate lua aceste valori mai mari și mai mici pe un interval și de mai multe ori (de exemplu -).
Se numește diferența dintre cele mai mari și cele mai mici valori ale unei funcții pe un segment ezitarefuncții pe un segment.
Proprietatea 3. (A doua teorema Bolzano - Cauchy). O funcție continuă pe un segment ia toate valorile între două valori arbitrare pe acest segment.
Proprietatea 4. Dacă funcția este continuă într-un punct, atunci există o vecinătate a punctului în care funcția își păstrează semnul.
Proprietatea 5. (Prima teoremă a lui Bolzano (1781-1848) - Cauchy). Dacă funcția este continuă pe un segment și are semne opuse la capetele segmentului, atunci există un punct în interiorul acestui segment, unde. și sunt aproape de zero.
la punctul funcția este continuă la punctul de discontinuitate de primul fel
Prelegerea 4.
Continuitatea funcțiilor
1. Continuitatea unei funcții într-un punct
Definiția 1.Să funcția y=f(x) este definit la punctul respectiv x 0 și în vreun cartier al acestui punct. Funcţie y=f(x) se numește continuu la punctul x 0 dacă există o limită a funcției în acest moment și este egală cu valoarea funcției în acest moment, adică
Astfel, condiția de continuitate pentru funcție y=f(x) la punct x 0 este asta:
pentru că 
, atunci egalitatea (32) poate fi scrisă în formă
(33)
Aceasta înseamnă că pentru găsirea limitei unei funcții continuef(x) puteți merge la limită sub semnul funcției, adică în funcțiune f(x) în loc de un argument x înlocuiți-i limita x 0 .
lim sin x\u003d păcat (lim x);
lim arctg x\u003d arctg (lim x); (34)
lim lоg x\u003d jurnal (lim x).
Sarcina.Găsiți limita: 1) 
;
2)
.
Să dăm o definiție a continuității unei funcții, bazată pe conceptul de argument și creșterea funcției.
pentru că condiții 
și 
sunt aceleași (Fig. 4), atunci egalitatea (32) ia forma:
sau 
.
Definiția 2. Funcţie y=f(x) se numește continuu la punctul x 0 , dacă este definit la punct x 0 și vecinătatea sa și un increment infinitesimal al argumentului corespunde unui increment infinitesimal al funcției.
Sarcina. Examinați continuitatea unei funcții y=2x 2 1.
Proprietăți ale funcțiilor care sunt continue într-un punct
1. Dacă funcțiile f(x) și φ
(x) sunt continue la punct x 0, apoi suma lor 
, compoziție 
și privat 
(dat fiind 
) sunt funcții continue la punct x 0 .
2. Dacă funcția la=f(x) este continuu la punct x 0 și f(x 0)\u003e 0, apoi există o vecinătate a punctului x 0 în care f(x)>0.
3. Dacă funcția la=f(tu) este continuu la punctul u 0, iar funcția u \u003d φ (x) este continuu la punct u 0 \u003d φ (x 0 ), apoi funcția complexă y=f[φ (x)] este continuu la punct x 0 .
2. Continuitatea funcției în interval și pe interval
Funcție y=f(x) se numește continuă în interval (a; b) dacă este continuu la fiecare punct al acestui interval.
Funcție y=f(x) se numește continuu pe segment
[a;
b] dacă este continuă în interval ( a;
b), și la punctul respectiv x=și este continuu pe dreapta (adică 
), și la punctul respectiv x=b este continuu pe stânga (adică 
).
3. Punctele de întrerupere ale unei funcții și clasificarea acestora
Se numesc punctele în care continuitatea funcției este ruptă puncte de rupere această funcție.
În cazul în care un x=x 0 point punct discontinuitate funcție y=f(x), atunci cel puțin una dintre condițiile primei definiții a continuității unei funcții nu este satisfăcută în ea.
Exemplu.
1.
. 2.
3)
4)
.
▼ Punct de întrerupere x 0 se numește punct de discontinuitate primul fel funcții y=f(x) dacă în acest moment există limite finite ale funcției în stânga și în dreapta (limite unilaterale), adică 
și 
... Unde:
Valoarea | A 1 -A 2 | numit funcția de salt la punctul de pauză de primul fel. ▲
▼ Punct de întrerupere x 0 se numește punct de discontinuitate al doilea fel funcții y=f(x) dacă cel puțin una dintre limitele unilaterale (stânga sau dreapta) nu există sau este egală cu infinitul. ▲
Sarcina. Găsiți puncte de întrerupere și aflați tipul acestora pentru funcții:
1)
;
2)
.
4. Teoreme de bază privind funcțiile continue
Teoremele privind continuitatea funcțiilor urmează direct din teoremele corespunzătoare asupra limitelor.
Teorema 1. Suma, produsul și coeficientul a două funcții continue este o funcție continuă (pentru coeficient, cu excepția acelor valori ale argumentului în care divizorul nu este zero).
Teorema 2. Lasă funcțiile tu=φ (x) este continuu la punct x 0 și funcția y=f(tu) este continuu la punct tu=φ (x 0 ). Apoi funcția complexă f(φ (x)), constând din funcții continue, este continuu la punct x 0 .
Teorema 3. Dacă funcția y=f(x) este continuu și strict monoton pe [ a; b] axă Oh, apoi funcția inversă la=φ (x) este, de asemenea, continuu și monoton pe segmentul corespunzător [ c;d] axă OU.
Orice funcție elementară este continuă în fiecare punct în care este definită.
5. Proprietățile funcțiilor continue pe un segment
Teorema Weierstrass. Dacă o funcție este continuă pe un segment, atunci atinge valorile sale maxime și minime pe acest segment.
Consecinţă. Dacă o funcție este continuă pe un segment, atunci este delimitată pe segment.
Teorema Bolzano-Cauchy.Dacă funcția y=f(x) este continuu pe segmentul [ a;
b] și ia valori inegale la capetele sale f(a)=A și f(b)=B,
apoi oricare ar fi numărul DINîncheiat între ȘI și ÎN,există un punct
astfel încât f(c)=C.
Geometric teorema este evidentă. Pentru orice număr DINîncheiat între ȘI și ÎN, există un punct cu interiorul acestui segment astfel încât f(DIN)=C... Drept la=DIN va intersecta graficul funcției cel puțin un punct.
Consecinţă. Dacă funcția y=f(x) este continuu pe segmentul [ a; b] și ia valori ale diferitelor semne la capetele sale, apoi în interiorul segmentului [ a; b] există cel puțin un punct dinîn care funcția y=f(x) dispare: f(c)=0.
Geometricsensul teoremei: dacă graficul unei funcții continue trece dintr-o parte a axei Oh la cealaltă, apoi traversează axa Oh.
Se încarcă ...